Interval-based methods are used in the field of mobile robotics to put reliable bounds on the results of different approaches (e.g. localization, map building, obstacle detection, …). These methods return an interval (lower and upper bound) containing the true solution. However, often such an interval is not sufficiently precise as it does not provide a working point as input for a controller.
Nevertheless, methods relying on interval analysis have many advantages over probabilistic approaches (e.g. guaranteed results under given assumptions, ability to model systematic errors, no linearization errors, …). They can be used to eliminate definitely wrong results while making no explicit statement about the true solution, which is only guaranteed to reside in the resulting interval. Naively, the midpoint of an interval can serve as a point-valued solution.
On the other hand, probabilistic approaches are widely used for different problems in the field of mobile robotics. By design, they return point-valued results, which, however, cannot be guaranteed and may be significantly wrong due to systematic or linearization errors. The aim of this project is to combine probabilistic and interval-based methods for robot control to guarantee the integrity of the solution. On the other hand, this enables us to provide point-valued results for further computations.
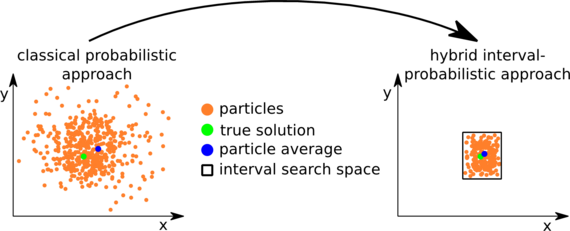
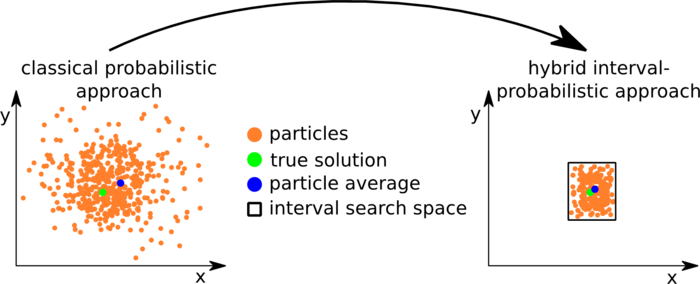
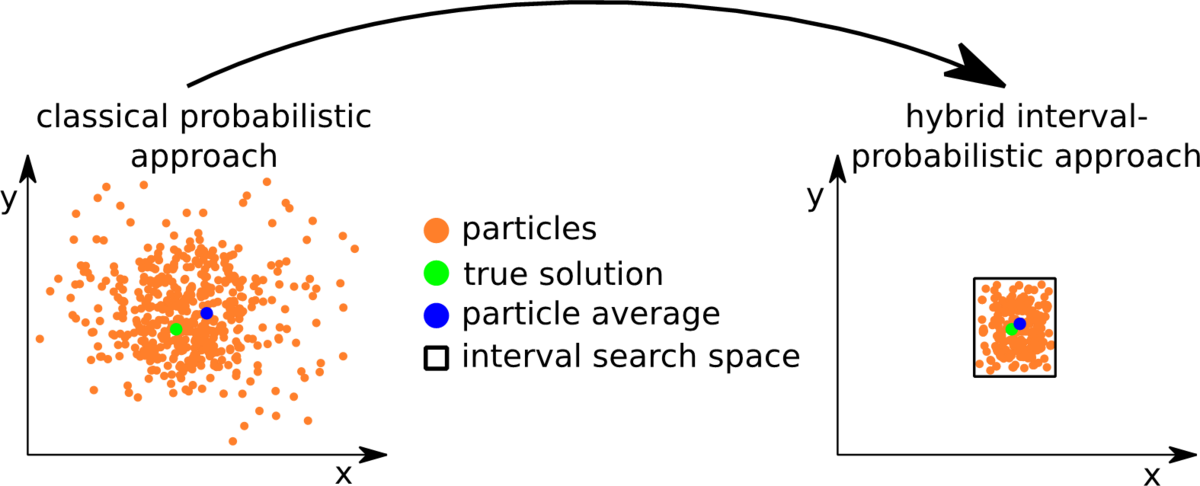
Appelstraße 9A
30167 Hannover