Supervisor: PD Dr.-Ing. Hamza Alkhatib
To deal with state estimation of Multi-Sensor-Systems (MSSs) and depending on the underlying assumptions, different possibilities exist. If the engaged probability distributions are assumed to be Gaussian, the Kalman filtering frameworks are typical to be used. Sometimes, it can happen that parts of the states have known probability distributions, whereas for some states only the boundaries are known. In the latter case, the probability distribution is unknown and only the state bounds are known to the user. In such a case, Sun et al. (2019) have proposed a new methodology called “Ellipsoidal and Gaussian Kalman Filter” in which the nonlinear models are overcome within an iterative process wherein the state uncertainties are described by optimal ellipsoids. The suggested framework can deal with cases where some states have Gaussian probability distributions and some other have only defined state bounds.
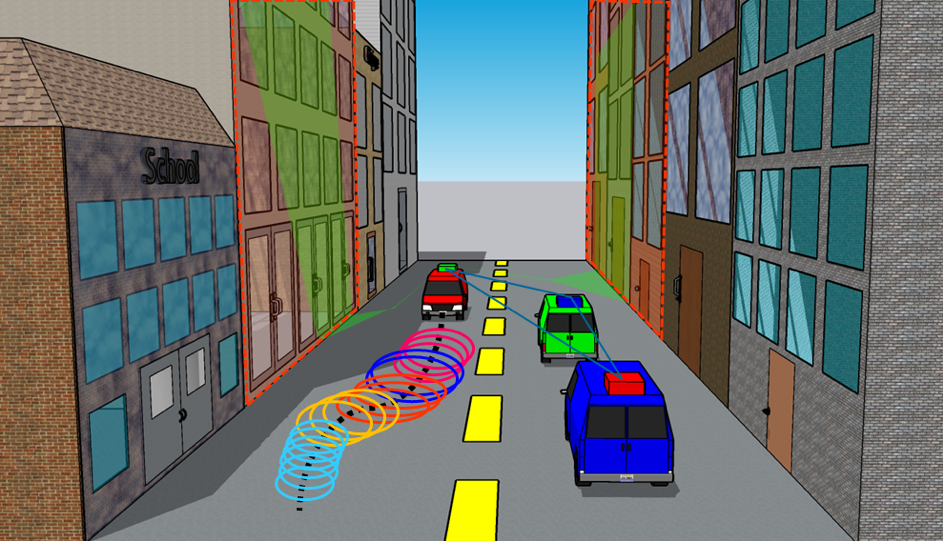
When it comes to real case studies, having always Gaussian distributions for the states is an optimistic assumption that cannot be always fulfilled. Usually, in real applications, the probability distribution of the states remains unknown. However, as suggested by Sun et al. (2019), in case of a prior knowledge, it is possible to have state boundaries without the necessity to know the underlying probability density function. On the other hand, the particle filter methodology is a typical framework in the context of localization, which is used to derive the states without imposing an unrealistic assumption of having Gaussian distributions. Moftizadeh et al. (2021) have proposed a particle filter algorithm – referred to as the “particle filter with implicit measurement equations” – which deals with the localization problem by considering different sensor data as well as additional information from the surrounding environment. Such additional information could be e.g. the existing building models within available digital 3D city models, or reliable height information given in digital terrain models. Moreover, the suggested particle filter methodology by Moftizadeh et al. (2021) considers cooperative positioning data that might have been exchanged between different nodes of a sensor network. An example of such a collaborative data are the measurements of Ultra-Wide-Bands (UWBs). These sensors deliver relative positioning information between different nodes, such as vehicles, infrastructures, etc.
Consequently, in the current project, the idea is to adapt the given methodology in Sun et al. (2019) to the suggested framework by Moftizadeh et al. (2021). Therefore, the resulting approach is a particle filter framework in which non-Gaussian distributions, e. g. the Student distribution, and boundary-based uncertainties can be handled via an optimal ellipsoid description of the uncertainties. Moreover, various sensor data following different observation model types (explicit and implicit) can be handled. Furthermore, additional information of the environment as well as state constraints can be taken into consideration. Finally, the resulting methodology can deal with concepts of integrity and collaborative positioning.
References
Sun L, Alkhatib H, Kargoll B, Kreinovich V, Neumann I. Ellipsoidal and Gaussian Kalman filter model for discrete-time nonlinear systems. Mathematics. 2019 Dec;7(12):1168.
Moftizadeh R, Vogel S, Dorndorf A, Jüngerink J, Alkhatib H. Information-Based Georeferencing of Multi-Sensor-Systems by Particle Filter with Implicit Measurement Equations. In2021 IEEE 24th International Conference on Information Fusion (FUSION) 2021 Nov 1 (pp. 1-8). IEEE.